What is a math hack?

I personally have started seeing them now that tik tok has took over most of my waking hours but they’ve existed for a while.

TLDR: It’s basically when someone shows you a semi involved operation and then shows some magic hack where you can fiddle with the numbers to arrive at the right solution via a simplier method. For example this pinterest link shows a hack for multiplying by any single digit number , the output turns out is always with the digits in the results added in and put in the middle. I.e. To compute we do which is and then you stick in the middle to get .

It works! Huzzah now if you ever need to specifically multiply 55 by a number you can. Now if your a normal person with a life and friends you go “huh neat” and move on with your day. I however, did not do that, i wondered why and how. Is this a actual rule i can use in day to day life? what are it’s limitations?

So i whipped out a pen and paper and tried to figure out the mechanics here and if there was a sorta mathematical proof.

I will note however that on one occasion my dad excitedly showed me a math hack and when i then got some paper and began to come up with a proof a lot of his excitement died so note that i am killing the magic here somewhat.

The 55 trick

To start lets quickly confirm this works for all 9 possibilites:

We had to take some liberties with since there is no “middle” to stick 5 into but it does seem to work. Formally it seems that if we have , then:

Now we can sub in to the and pretty quickly prove that the equation holds for all real values of and .

Which was…suprising to me. If this is correct then this should work for bigger as well? What about ? Well if then:

Huh. The above notation kinda gives away the underlying reason this works. This, and frankly a lot of math hacks, boil down into the fact that we work with a decimal system and we can very easily break numbers down into 100s and 10s and 1s and recombine them. Showing someone the formula

where

Is unlikely to make anyone go “woah! how easy!” but is a easy computation and finding and are trivial for 2 digit numbers, you just take the first and second digit as and . You can explain as taking and , adding them and sticking it in the middle of thw two. Visually it seems like we are just moving numbers around but when we put 3 single digits next to each other as we are actually just very quickly computing . This is the exact same reasoning.

All we’ve really done here is broken down into a form where we can repesent it in terms of 100s, 10s and 1s and if you lean into this idea you can imagine how we could have arrived at it ourselves:

Hrm but 5n could be multiple digits which is hard, lets break it down into it’s consitute digits:

And we’re at our formula again!

Generalising

You may have noticed that the doesn’t seem to be incredibly special. What’s nice is that you can break 55 down into but wait, this is true of all multiples of . in fact is a very magic number and you’ll see it in a couple of different math hacks, each for the same reason.

In fact lets generalise our equation from above.

where

But try and you’ll see why this pinterest post did not use 88.

The moment your “middle” value is more then 1 digit it breaks! You can’t just stick it in between and . If you think back to the underlying math here you can quickly see why. You aren’t saying “stick 12 in the middle” you are actually saying “the result has 4 hundreds, 12 tens and 8 ones”. Thinking about it this way you can quickly adjust the hack to up the number of hundreds by 1 and you get to .

I find this view of the hack to actually be a lot better then the approach a lot of videos take where they just show you numbers moving around, a slightly deeper understanding means you can use these hacks in more situations without getting confused.

The fingers trick

This one is a trick for your 9 times tables. It was lovingly explained to me as so:

4x9? Simply spread all your fingers out, then put the 4th one down. What do you have left on either side of the one that’s down? 3 on the left and 6 on the right. 36

Why does it work?

This one is quite satisfying to look at, where has this nice property of always consisting of 2 digits that add up to :

If you know you can get pretty quickly by adding one to the first digit and subtracting 1 from the second. How come? Well once again lets think about this in terms of 10s and 1s.

can be written as , that is to say that the number of 10s in the output of will always be as we would compute then subtract 1 or more from it, bumping it down. This immediately gives us the rationale for why picking your nth finger and looking at the number of fingers before it gives us the first digit of our answer. We’re just doing .

Now the second digit consistently reduces by 1 for each increase in , of course it does, the equation has a afterall. The finger trick encodes this logic, by chosing the th finger, you reduce the number of fingers after it by 1.

The finger trick is just a quick way to compute for . Cheeky isn’t it!

Line Multiplication

This one is kinda fun because it lets you solve complex multiplications more visually. Consider :

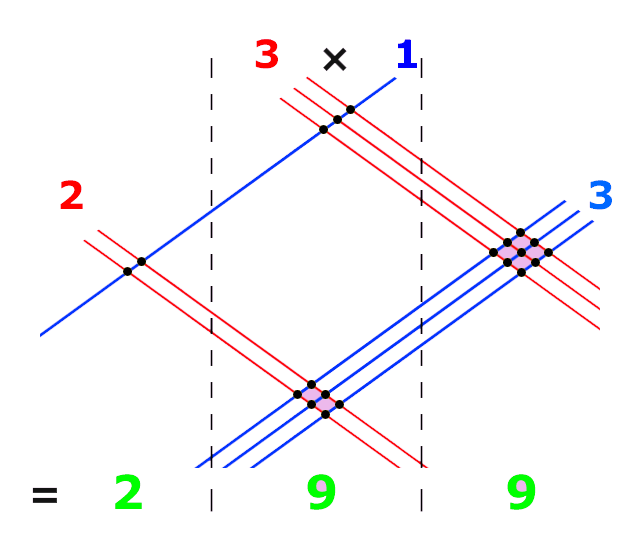
This is apparently a trick that they teach is japan, although i read that online so who knows if that’s remotely true. Once again the trick here is breaking the problem down into single digit operators and using the visual representation to handle the 100s, 10s and 1s.

Generalising for any two numbers, each 2 digits:

The line method just encodes this formula in a easier to remember way. You might feel like this is familar and if you were taught the FOIL method it very much is!

Conclusion

I dunno i thought this was interesting. Bye!